- 1.1. Selection sort
- 1.2. Bubble sort
- 1.3. Insertion sort
- 1.4. Quick sort
- 1.5. Merge sort
- 1.6. Heap sort
- 1.7. Depth First Search(DFS) for binary search
- 1.8. Binary Search
Python Algorithm Practice
select/bubble/quick/merge/radix
import random
arr = random.sample(range(1,11),10)
size = len(arr)
k = 1 # search 1st
1.1. Selection sort
for i in range(0,size-1):
min_idx = i
for j in range(i+1, size):
# print(i,j)
if (arr[j] < arr[min_idx]):
min_idx = j
arr[min_idx], arr[i] = arr[i], arr[min_idx]
print(arr[k])
1.2. Bubble sort
for end in range(size-1, 0, -1):
for i in range(end):
# print(end, i)
if arr[i] > arr[i+1]:
arr[i], arr[i+1] = arr[i+1], arr[i]
print(arr[k])
1.3. Insertion sort
for end in range(size):
for i in range(end, 0, -1):
# print(end, i)
if arr[i-1] > arr[i]:
arr[i-1], arr[i] = arr[i], arr[i-1]
print(arr[k])
1.4. Quick sort
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[0]
lesser_arr, equal_arr, greater_arr = [], [], []
for i in arr:
if i < pivot:
lesser_arr.append(i)
elif i > pivot:
greater_arr.append(i)
else:
equal_arr.append(i)
print(lesser_arr, equal_arr, greater_arr)
return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)
quick_sort(arr)
1.5. Merge sort
def merge_sort(arr):
if len(arr) < 2:
return arr
mid = len(arr) // 2
low_arr = merge_sort(arr[:mid])
high_arr = merge_sort(arr[mid:])
merged_arr = []
l = h = 0
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l +=1
else:
merged_arr.append(high_arr[h])
h += 1
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
print(merged_arr)
return merged_arr
merge_sort(arr)
1.6. Heap sort
# subtree rooted at index i.
def heapify(arr, n, i):
largest = i # Initialize largest as root_i
l = 2*i + 1 # left = 2*i + 1
r = 2*i + 2 # right = 2*i + 2
if l < n and arr[i] < arr[l]:
largest = l
if r < n and arr[largest] < arr[r]:
largest = r
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
heap_size = len(arr)
# 1) Build a maxheap.
# Since last parent will be at ((heap_size//2)-1) we can start at that location.
for root_i in range((heap_size//2)-1, -1, -1):
heapify(arr, heap_size, root_i)
# 2) One by one extract elements
for i in range(n-1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 가장 큰 값을 마지막으로 이동 후 build a maxheap 반복
heapify(arr, i, 0)
print(arr)
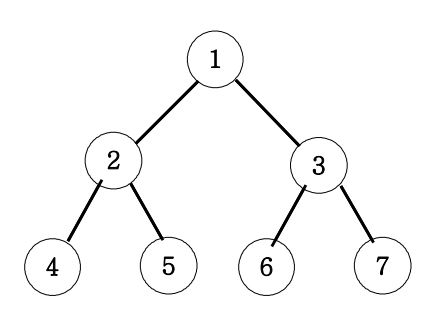
1.7. Depth First Search(DFS) for binary search
Preorder Traversal
root -> left -> right
전위순회 출력 : 1 2 4 5 3 6 7
def traversal(num):
if num > 7: return
else:
print(num, end=' ')
traversal(num*2)
traversal(num*2+1)
traversal(1)
Inorder Traversal
left -> root -> right
중위순회 출력 : 4 2 5 1 6 3 7
def traversal(num):
if num > 7: return
else:
traversal(num*2)
print(num, end=' ')
traversal(num*2+1)
traversal(1)
Preorder Traversal
left -> right -> root
후위순회 출력 : 4 5 2 6 7 3 1
def traversal(num):
if num > 7: return
else:
traversal(num*2)
traversal(num*2+1)
print(num, end=' ')
traversal(1)
1.8. Binary Search
input: 7
3
5
2
1
4
6
7
class Node:
def __init__(self,data):
self.right=self.left=None
self.data = data
print(f"{data} node created")
class Solution:
def insert(self,root,data):
if root==None:
return Node(data)
else:
print(f'data:{data}, root.data:{root.data}')
if data<=root.data:
cur=self.insert(root.left,data)
root.left=cur
else:
cur=self.insert(root.right,data)
root.right=cur
return root
def getHeight(self,root):
if root == None:
return -1
else:
return 1 + max(self.getHeight(root.left), self.getHeight(root.right))
T=int(input())
myTree=Solution()
root=None
for i in range(T):
data=int(input())
root=myTree.insert(root,data)
height=myTree.getHeight(root)
# print(height) # tree 높이 구하기
> 결과
3 node created
data:5, root.data:3
5 node created
data:2, root.data:3
2 node created
data:1, root.data:3
data:1, root.data:2
1 node created
data:4, root.data:3
data:4, root.data:5
4 node created
data:6, root.data:3
data:6, root.data:5
6 node created
data:7, root.data:3
data:7, root.data:5
data:7, root.data:6
7 node created