R과 함께하는 통계학의 이해 - 최용석
3.1 사건의 확률
확률(probability) : 실험의 결과에 대해 확신하는 정도를 수치적으로 나타는 척도
사건(event) : 어떤 특성을 갖는 결과들의 집합을 ($A$, $B$, …)
3.2. 확률변수
확률변수(random variable) : 표본공간에 속하는 각각의 결과들에 대해 실수값 대응 시켜준 변수 ($X$, $Y$, …)
- 한주에 경기 수 (0회, 1회, 2회)
확률변수가 가지는 특정값 : ($x$, $y$, …)
가질 수 있는 값에 따라,
1) 이산확률변수(discrete random variable)
2) 연속확률변수(continuous random variable)
3.3 이산확률변수의 확률분포함수
확률분포(probability distribution) : 확률변수가 가지는 값과 그 값을 가질 확률을 정해주는 규칙
- 한주의 경기 수와 그 비율 (0회: $\frac{2}{10}$, 1회: $\frac{5}{10}$, 2회: $\frac{3}{10}$)
(이산확률변수의) 확률분포함수(probability distribution function) :
$ f(x)= P(X=x) $
이산 확률분포함수의 성질
모든 $x$값에 대해 $0 \leq f(x) \leq 1$
$ \sum f(x) =1 $
3.4 확률변수의 기대값과 표준편차
확률변수의 기대값(expected value) : 확률변수가 가질 수 있는 값들에 대한 확률분포 상의 중심위치
$ E(X) = \sum xf(x)$
- 평균적으로 한주에 수행하는 경기 수 ($ 0회 \times \frac{2}{10} + 1회 \times \frac{5}{10} + 2회 \times \frac{3}{10} = 1.1회$ )
평균과 다른 점? 기대값은 동일한 실험을 무수히 반복했을 때의 평균을 의미하고 10회 던져서 8번 나왔다고 0.8이라고 하지 않음
실수값을 갖는 확률변수에 대해서, 모평균은 확률변수의 기대값이 된다.
기대값의 성질
$ E(X) = \mu $
$ E(a) = a $
$ E(aX) = a\mu $
$ E(aX \pm b) = a\mu \pm b$
확률변수의 분산(variance)
- 평균적으로 한주에 수행하는 경기 수의 분산 ($ (0회-1.1회)^2 \times \frac{2}{10} + (1회-1.1회)^2 \times \frac{5}{10} + (2회-1.1회)^2 \times \frac{3}{10} = 0.49 $ )
$ Var(X) = \sum (x-\mu)^2f(x)$
$ Var(X) = E[ (X - E(X) )^2 ] $
$ Var(X) = E(X^2) - E(X)^2 $
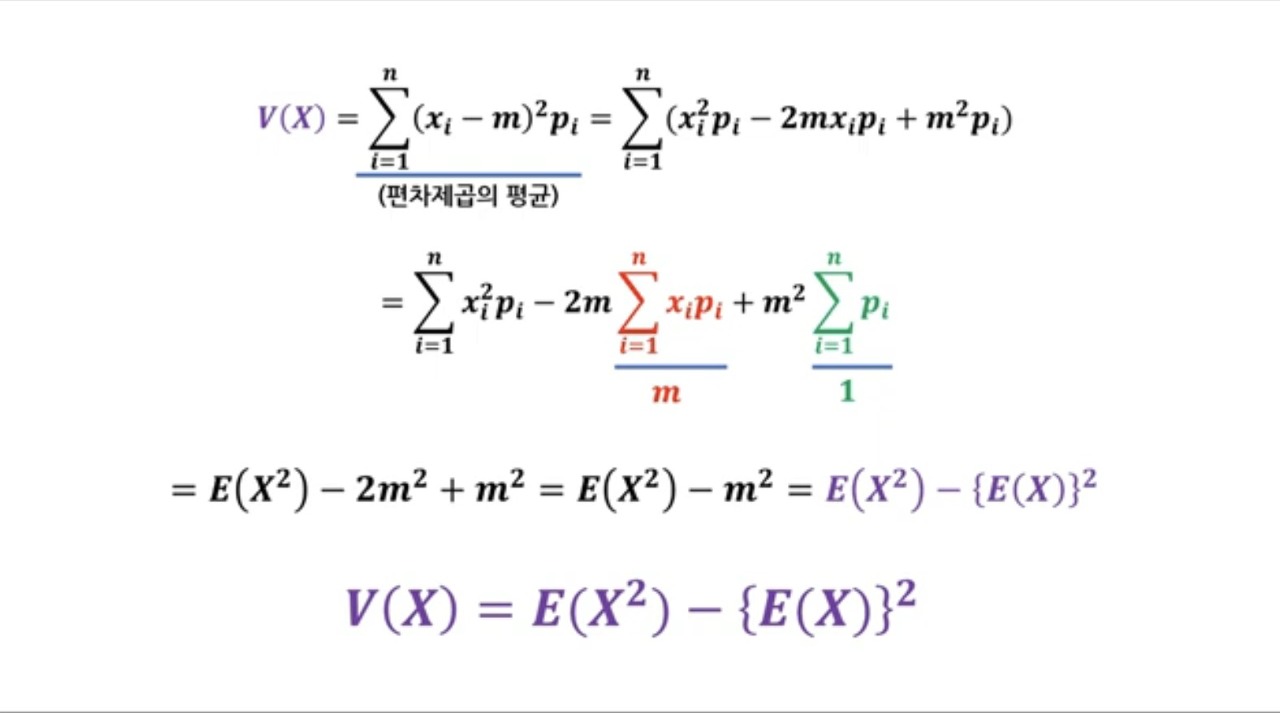
분산의 성질
$ Var(X) = \sigma^2 $
$ Var(a) = 0 $
$ Var(aX) = a^2\sigma^2 $
$ Var(aX \pm b) = a^2\sigma^2 $
확률변수의 표준편차(standard deviation)
$ \sqrt{ Var(X) } = \sqrt{ \sum (x-\mu)^2f(x) } $
3.5 이항분포
3.3에서 확률분포란 확률변수가 가지는 값과 그 값을 가질 확률을 정해주는 규칙이라고 정의하였는데, 규칙이 밝혀져 이름이 부여된 것들이 있는데 대표적인 예가 이항분포
베르누이 시행 : 단 1회의 실험 지칭
베르누이 시행의 특징
- 각 시행은 성공(success, $S$ )과 실패(fail, $F$ )의 두 가지 결과만을 갖는다.
- 각 시행에서 성공할 확률은 $P(S)$ , 실패할 확률은 $P(F)$ 로 매 시행마다 동일하다.
- 각 시행은 상호 독립으로 각각의 시행이 다른 시행의 결과에 영향을 미치지 않는다.
성공 확률이 $p$인 베르누이 시행을 $n$번 시행한 경우 성공 횟수를 나타내는 확률변수 $X$의 확률분포함수는
$ f(x) = P(X=x) = _{n}C_{x}p^x(1-p)^{n-x} , x=0,1,…,n$
이항부포의 기대값과 분산
성공 횟수를 나타내는 확률변수 $X$가 $X ~ Bin(n,p)$일 때,
$ E(X) = np $
$ E(X) = np(1-p) $
