4.1 연속확률변수의 확률분포함수

연속확률변수: 확률변수가 특정 구간의 모든 값을 다 가질 수 있기 때문에 가질 수 있는 값들을 일일이 지칭할 수 없는 확률변수를 의미

연속확률분포함수: 확률변수 $X$가 가질 수 있는 특정 구간에서 확률이 어떻게 분포하는가를 나타낼 수 있는 함수

$X$의 확률분포는 확률의 밀도를 나타내는 확률밀도함수

확률밀도함수(probability density function)

모든 $x$에 대해 $f(x) \geq 0 $
$P(a \leq X \leq b) = \int_{a}^{b}{f(x)dx}$
$P(\infty \leq X \leq -\infty) = \int_{\infty}^{-\infty}{f(x)dx} = 1$

연속확률변수 $X$가 특정한 값 $x$를 갖게 되는 확률은 0이므로, 구간의 확률을 구할 때는 그 구간의 경계점의 포함 유무는 영향을 받지 않는다.

연속확률변수의 기대값과 분산

$ E(X) = \int{xf(x)dx} $
$ Var(X) = \int{(x-\mu)^2f(x)dx} = \sigma^2 $

4.2 정규분포

정규분포(normal distribution): 좌우대칭의 종모양 곡선 (=Gaussian distribution)

정규확률변수 : 종 모양의 확률밀도함수를 가지는 연속형확률변수 X

정규확률변수의 확률분포에 대한 식은 모집단에 대한 평균 $\mu$와 분산 $\sigma^2$에 의존하므로
$ X \sim N(\mu, \sigma^2) $ 로 표기

4.3 정규분포의 확률계산

표준정규분포(standard normal distribution): 평균이 0이고, 분산이 1인 정규분포

일반적으로 표준정규분포를 따르는 확률변수는 $Z$로 표현
$ Z \sim N(0,1) $이므로 확률변수 $Z$는
평균 $E(Z) = \mu_z = 0 $이며, 분산은 $ Var(Z) = \sigma_z^2 = 1 $과 같다.

일반적인 정규분포를 따르는 확률변수 $X$에 대한 확률을 표준정규분포를 따르는 확률변수 $Z$로 변환하는 과정을 표준화(Standardization)라고 한다.

$ \frac{X-\mu_x}{\sigma_x} $

4.4 이항분포의 정규근사

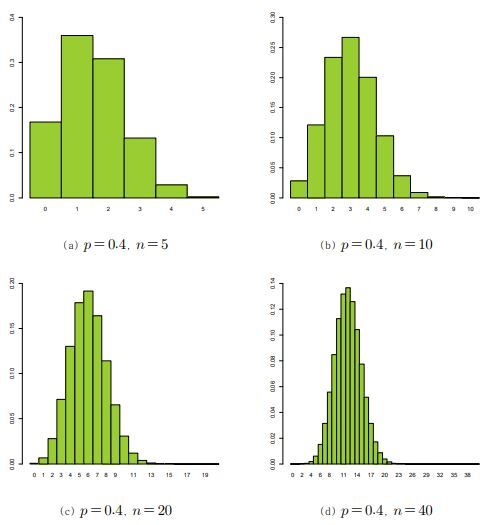
$n$이 증가함에 따라 분포의 형태가 점차 좌우대칭의 종 모양에 가까워짐을 확인할 수 있다.

이항분포의 정규근사

확률변수 $X$가 성공 횟수를 나타내는 이산형 확률변수이고 $X \sim Bin(n,p) $일 때,
$np$나 $n(1-p)$이 모두 충분히 클 경우(보통 10 이상)에 확률변수 $X$는 근사적으로 다음의 정규 분포를 따르게 된다.
$ X \sim N(np, np(1-p)) $