younghunjo1 blog Python and R Tips

06_통계분석_3 (QDA, MDS, CA)

판별분석 QDA(Quadratic Discriminant Analysis)

선형판별분석(LDA), 이차판별 분석(QDA)은 확률론적 생성모형

LDA (Linear Discriminant Analysis)

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
y = np.array([1, 1, 1, 2, 2, 2])

clf = LinearDiscriminantAnalysis()

clf.fit(X, y)


print(clf.predict([[-0.8, -1]]))

[2]

QDA (Quadratic Discriminant Analysis)

from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
quad_clf = QuadraticDiscriminantAnalysis()
quad_clf.fit(X, y)

print(clf.predict([[-0.8, -1]]))

[2]

from sklearn.metrics import confusion_matrix

y_pred = clf.predict(X)
confusion_matrix(y, y_pred)
y_pred2 = quad_clf.predict(X)
confusion_matrix(y, y_pred2)


QuadraticDiscriminantAnalysis()

from sklearn.datasets import make_moons, make_circles, make_classification
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
%matplotlib inline

h=0.2
names = ["LDA", "QDA"]
classifiers = [
    LinearDiscriminantAnalysis(),
    QuadraticDiscriminantAnalysis()]

X, y = make_classification(n_features=2, n_redundant=0, n_informative=2,
                           random_state=1, n_clusters_per_class=1)
rng = np.random.RandomState(2)
X += 2 * rng.uniform(size=X.shape)
linearly_separable = (X, y)

datasets = [make_moons(noise=0.3, random_state=0),
            make_circles(noise=0.2, factor=0.5, random_state=1),
            linearly_separable
            ]

figure = plt.figure(figsize=(27, 9))
i = 1
# iterate over datasets
for ds in datasets:
    # preprocess dataset, split into training and test part
    X, y = ds
    X = StandardScaler().fit_transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4)

    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # just plot the dataset first
    cm = plt.cm.RdBu
    cm_bright = ListedColormap(['#FF0000', '#0000FF'])
    ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
    # Plot the training points
    ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
    # and testing points
    ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright, alpha=0.6)
    ax.set_xlim(xx.min(), xx.max())
    ax.set_ylim(yy.min(), yy.max())
    ax.set_xticks(())
    ax.set_yticks(())
    i += 1

    # iterate over classifiers
    for name, clf in zip(names, classifiers):
        ax = plt.subplot(len(datasets), len(classifiers) + 1, i)
        clf.fit(X_train, y_train)
        score = clf.score(X_test, y_test)

        # Plot the decision boundary. For that, we will assign a color to each
        # point in the mesh [x_min, m_max]x[y_min, y_max].
        if hasattr(clf, "decision_function"):
            Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
        else:
            Z = clf.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1]

        # Put the result into a color plot
        Z = Z.reshape(xx.shape)
        ax.contourf(xx, yy, Z, cmap=cm, alpha=.8)

        # Plot also the training points
        ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cm_bright)
        # and testing points
        ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=cm_bright,
                   alpha=0.6)

        ax.set_xlim(xx.min(), xx.max())
        ax.set_ylim(yy.min(), yy.max())
        ax.set_xticks(())
        ax.set_yticks(())
        ax.set_title(name)
        ax.text(xx.max() - .3, yy.min() + .3, ('%.2f' % score).lstrip('0'),
                size=15, horizontalalignment='right')
        i += 1

figure.subplots_adjust(left=.02, right=.98)
plt.show()

png



MultiDimensional Scaling (MDS) 다차원척도법

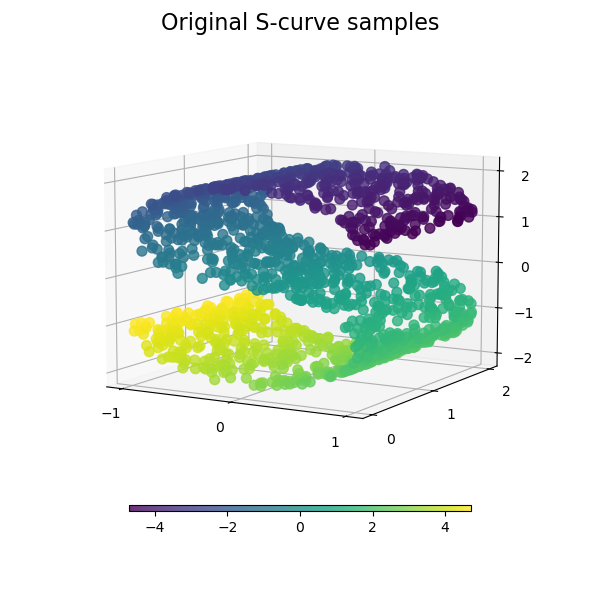
여러 차원 축소 기법 중 하나 차원축소예시들

종류

1) 계량적: PCoA (principle coordinates analysis)
Classical multidimensional scaling으로, PCA (principle component analysis)와 매우 비슷하나,
PCA: Euclidean 거리 사용하고 선형 관계 있으면 사용 (대부분 geological data)
PCoA: Euclidean 거리 외 다른 측정방법 사용하고 선형 관계 있으면 사용 (biogeographic data)

2) 비계량적: Non-MultiDimensional Scaling (NMDS)
NMDS: Euclidean 거리 외 다른 측정방법 사용하고 선형 관계 없으면 사용 (어떤 지역 species 개체 수 많은 지)

계량적(구간척도, 비율척도)

mds 객체 생설할 때 dissimilarity로 euclidean할지 precomputed 미리 계산된 걸로 할 지 정하고
mds.fit_transform 옵션에서 계산된 manhattan_distances 넣어주면 됨

from sklearn.manifold import MDS
from matplotlib import pyplot as plt
import sklearn.datasets as dt
import seaborn as sns         
import numpy as np
from sklearn.metrics.pairwise import manhattan_distances, euclidean_distances
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
from sklearn.datasets import load_digits

X2 = np.array([[0, 0, 0], [0, 0, 1], [1, 1, 1], [0, 1, 0], [0, 1, 1]])

mds2 = MDS(random_state=0)
X2_transform = mds2.fit_transform(X2)
print(X2_transform)

stress2 = mds2.stress_
print(stress2)

[[ 0.72521687  0.52943352]
 [ 0.61640884 -0.48411805]
 [-0.9113603  -0.47905115]
 [-0.2190564   0.71505714]
 [-0.21120901 -0.28132146]]
0.18216844548575456

stress는 잘 피팅되었는지 검증용으로, 계산된 거리가 dissimilarity 차이를 보여주는데

stress가 통상 0.2 이상이면 차원 높여야 함

# plt.scatter([1,2,3,4], [10,30,20,40], s=[30,60,90,120], c=range(4), cmap='jet')
# plt.colorbar()


colors = ['r', 'g', 'b', 'c', 'm']
size = [64, 64, 64, 64, 64]
fig = plt.figure(2, (10,4))

ax = fig.add_subplot(121, projection='3d')
plt.scatter(X2[:,0], X2[:,1], zs=X2[:,2], s=size, c=colors)
plt.title('Original Points')

ax = fig.add_subplot(122)
plt.scatter(X2_transform[:,0], X2_transform[:,1], s=size, c=colors)
plt.title('Embedding in 2D')
fig.subplots_adjust(wspace=.4, hspace=0.5)
plt.show()

png

dist_manhattan = manhattan_distances(X2)
mds3 = MDS(dissimilarity='precomputed', random_state=0)
# Get the embeddings
X2_transform_L1 = mds3.fit_transform(dist_manhattan)
print(X2_transform_L1)
print(mds3.stress_)

[[ 0.9847767   0.84738596]
 [ 0.81047787 -0.37601578]
 [-1.104849   -1.06040621]
 [-0.29311254  0.87364759]
 [-0.39729303 -0.28461157]]
0.4047164940033806

fig = plt.figure(2, (15,6))

ax = fig.add_subplot(131, projection='3d')
plt.scatter(X2[:,0], X2[:,1], zs=X2[:,2], s=size, c=colors)
plt.title('Original Points')

ax = fig.add_subplot(132)
plt.scatter(X2_transform[:,0], X2_transform[:,1], s=size, c=colors)
plt.title('Embedding in 2D')
fig.subplots_adjust(wspace=.4, hspace=0.5)

ax = fig.add_subplot(133)
plt.scatter(X2_transform_L1[:,0], X2_transform_L1[:,1], s=size, c=colors)
plt.title('Embedding in 2D L1')
fig.subplots_adjust(wspace=.4, hspace=0.5)

plt.show()

png

# print(load_digits.__doc__)
X, y = load_digits(return_X_y=True)
X = X[:100]
print(X.shape)

mds = MDS(n_components=2)
X_transformed = mds.fit_transform(X[:100])
print(X_transformed.shape)
Y = y[:100]
print(Y.size)
# print(X_transformed[:5,0])
# print(X_transformed[:5,1])
print(mds.stress_)

(100, 64)
(100, 2)
100
1133807.722583498

colormap = np.array(['b', 'g', 'r', 'c', 'm', 'y', 'k', 'w', 'w', 'w'])
# colormap[Y]
fig = plt.figure(2, (10,4))

ax = fig.add_subplot(122)
plt.scatter(X_transformed[:,0], X_transformed[:,1], c=colormap[Y])
plt.title('Embedding in 2D')
plt.show()

png

nmds = MDS(n_components=2, metric=False)
nX_transformed2 = nmds.fit_transform(X)
# print(nX_transformed2)
nX_transformed2 *= np.sqrt((X ** 2).sum()) / np.sqrt((nX_transformed ** 2).sum())
# print(nX_transformed2)
Y = y[:100]
# print(Y.size)
# print(nX_transformed[:5,0])
# print(nX_transformed[:5,1])
# print(nmds.stress_)

colormap = np.array(['b', 'g', 'r', 'c', 'm', 'y', 'k', 'w', 'w', 'w'])
# colormap[Y]
fig = plt.figure(2, (10,4))

ax = fig.add_subplot(122)
plt.scatter(nX_transformed2[:,0], nX_transformed2[:,1], c=colormap[Y])
plt.title('Embedding in non mds 2D')
plt.show()

png

non-metric MDS: 다차원척도법 비계량적(순서척도)

1) 차이에 대해 수치화(quantified) 한 값을 얻기 힘들때, 순서만 알 수 있을 때 사용
예) 검정색-진회색-연회색-흰색… 중 가장 밝은 색, 빈도 수가 많은 데이터

2) 유클리디안 외 user-selected 거리 메트릭을 사용하고 싶을 때 (Jaccard,…)

Metric = False 옵션 주면 됨.

3) 차원이 미리 결정되어야 하고, local minima(지역 최소값) 수렴 가능성이 있고, 시간 오래 걸리는 게 단점


from sklearn.preprocessing import MinMaxScaler
from mpl_toolkits import mplot3d


df = pd.read_csv('../data/yeast-transcriptomics/SC_expression.csv')
df = df.iloc[:,1:]
# print(df.corr())
# print(df.T)
df1 = df.T.values
sc = MinMaxScaler()
scaled = sc.fit_transform(df1)
# print(scaled)
mds = MDS(n_components=2)
mds_scaled = mds.fit_transform(scaled)
nmds = MDS(n_components=2, metric=False)
nmds_scaled = nmds.fit_transform(scaled)

plt.subplot(121)
sns.scatterplot(x=mds_scaled[:,0],y=mds_scaled[:,1])
plt.legend(loc='best')
plt.title('MDS')

plt.subplot(122)
sns.scatterplot(x=nmds_scaled[:,0],y=nmds_scaled[:,1])
plt.legend(loc='best')
plt.title('nMDS')



No handles with labels found to put in legend.
No handles with labels found to put in legend.





Text(0.5, 1.0, 'MDS')

png



CA (Correspondence Analysis) - 대응분석

차원 축소 기법

1. Feature Extraction

supervised/unsupervised는 Y값의 분산 활용 유무로 나뉨

Unsupervised: PCA, AutoEncoder

PCA는 X라는 독립변수들의 간의 선형결합으로 추출된 새로운 변수 추출

Supervised: PLS(부분 최소제곱법)

PLS는 X라는 독립변수들의 선형결합과 Y라는 종속변수 이 2개 간의 공분산을 최대화 하는 새로운 변수 추출함
PCA의 일반적인 선형결합으로 추출된 새로운 변수가 설명하지 못하는 부분에 반복적으로 최소제곱법을 적용함

2. Feature Selection

Unsupervised: PCA loading

Supervised: Information Gain, Stepwise, Losso regression, Genetic algorithm

대응분석

PLS 군에 속하는 차원축소 방법
다변량 범주형 자료 대상으로 탐색적 분석 시 사용
분할표에서 행과 열의 범주들간의 대응 관계를 탐구하기 위해 2차원 공간상 관계로 시각화

python은 big data, ML용으로 많이 사용되므로 상대적으로 데이터 양이 한정적인 대응분석은 잘 사용하지 않는 듯함

Homogeneity (동질성): 각 행에 대해 열의 분포가 동일한가?
Independence (독립성): 두 범주형 변수(X,Y)는 서로 독립인가?
이원분할표 -> 단순대응분석 (독립성, 동질성 검정 -> chi-squared test)
다원분할표 -> 다중대응분석 (chi-squared test 신뢰도가 떨어지므로 )

PCA vs CA

PCA: 많은 종의 생물에서 패턴 찾을 때

CA: 생물 종간의 상대적인 패턴을 찾을 때

예)
A = {50,20,10}
B = {5,2,1}
PCA의 경우 A와 B를 완전 다르다고 판단 (유클리디안 거리 측정법 사용)
CA의 경우 A와 B가 비슷하다고 판단

chi-squared test vs CA

chi-squared test: 두 범주형 변수간의 연관성을 찾을 떄,

CA: 두 변수가 가지고 있는 범주들 사이의 관계를 찾을 때, 두 개 이상의 범주 군 사이의 상관성을 분석하는 기법

예)
X = df[[‘bill_length_mm’,’bill_depth_mm’]]
Y = df[[‘flipper_length_mm’,’body_mass_g’]]
chi-squared test로는 X와 Y의 독립성 검정을 실시하고, 두 group간에는 상당히 연관 관계가 있다고 판단까지
CA로는 X와 Y의 group내에서 어떤식으로 연관관계가 있는지 판단

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from sklearn.cross_decomposition import CCA #Canonical Correlation Analysis

link2data = "https://raw.githubusercontent.com/mwaskom/seaborn-data/master/penguins.csv"
df = pd.read_csv(link2data)
df =df.dropna()
print(df.head())

# pre-processing
X = df[['bill_length_mm','bill_depth_mm']]
# print(X.head())
X_mc = (X-X.mean())/(X.std())
print(X_mc.head())

Y = df[['flipper_length_mm','body_mass_g']]
# print(Y.head())
Y_mc = (Y-Y.mean())/(Y.std())
print(Y_mc.head())

  species     island  bill_length_mm  bill_depth_mm  flipper_length_mm  \
0  Adelie  Torgersen            39.1           18.7              181.0   
1  Adelie  Torgersen            39.5           17.4              186.0   
2  Adelie  Torgersen            40.3           18.0              195.0   
4  Adelie  Torgersen            36.7           19.3              193.0   
5  Adelie  Torgersen            39.3           20.6              190.0   

   body_mass_g     sex  
0       3750.0    MALE  
1       3800.0  FEMALE  
2       3250.0  FEMALE  
4       3450.0  FEMALE  
5       3650.0    MALE  
   bill_length_mm  bill_depth_mm
0       -0.894695       0.779559
1       -0.821552       0.119404
2       -0.675264       0.424091
4       -1.333559       1.084246
5       -0.858123       1.744400
   flipper_length_mm  body_mass_g
0          -1.424608    -0.567621
1          -1.067867    -0.505525
2          -0.425733    -1.188572
4          -0.568429    -0.940192
5          -0.782474    -0.691811

ca = CCA()
ca.fit(X_mc, Y_mc)
X_c, Y_c = ca.transform(X_mc, Y_mc)
print(X_c[:5])
print(Y_c[:5])

[[-1.18625232 -0.01036701]
 [-0.70957262 -0.4560358 ]
 [-0.79073194 -0.13080943]
 [-1.7186634  -0.07362316]
 [-1.77229457  0.73624799]]
[[-1.40879506  0.68286617]
 [-1.05385671  0.42987851]
 [-0.3935502  -0.83961988]
 [-0.5428878  -0.45857086]
 [-0.76354771 -0.01420367]]

cc_res = pd.DataFrame({"CCX_1":X_c[:, 0],
                       "CCY_1":Y_c[:, 0],
                       "CCX_2":X_c[:, 1],
                       "CCY_2":Y_c[:, 1],
                       "Species":df.species.tolist(),
                      "Island":df.island.tolist(),
                      "sex":df.sex.tolist()})
print(cc_res.head())

print(np.corrcoef(X_c[:, 0], Y_c[:, 0])) # 첫번째 변수끼리의 공분산
print(np.corrcoef(X_c[:, 1], Y_c[:, 1])) # 두번째 변수끼리의 공분산

      CCX_1     CCY_1     CCX_2     CCY_2 Species     Island     sex
0 -1.186252 -1.408795 -0.010367  0.682866  Adelie  Torgersen    MALE
1 -0.709573 -1.053857 -0.456036  0.429879  Adelie  Torgersen  FEMALE
2 -0.790732 -0.393550 -0.130809 -0.839620  Adelie  Torgersen  FEMALE
3 -1.718663 -0.542888 -0.073623 -0.458571  Adelie  Torgersen  FEMALE
4 -1.772295 -0.763548  0.736248 -0.014204  Adelie  Torgersen    MALE
[[1.         0.78763151]
 [0.78763151 1.        ]]
[[1.         0.08638695]
 [0.08638695 1.        ]]

fig = plt.figure(figsize=(15,5))
sns.set_context("talk", font_scale=1.2)

fig.add_subplot(121)
sns.scatterplot(x="CCX_1",
                y="CCY_1", 
                hue="Species",
                data=cc_res)
plt.title('Comp. 1, corr = %.2f' %
         np.corrcoef(X_c[:, 0], Y_c[:, 0])[0, 1])

fig.add_subplot(122)
sns.scatterplot(x="CCX_2",
                y="CCY_2", 
                hue="Species", data=cc_res)
plt.title('Comp. 2, corr = %.2f' %
         np.corrcoef(X_c[:, 1], Y_c[:, 1])[0, 1])

# fig.add_subplot(122)
# sns.scatterplot(x="CCX_2",
#                 y="CCY_2", 
#                 hue="sex", data=cc_res)
# plt.title('Second Pair of Canonical Covariate, corr = %.2f' %
#          np.corrcoef(X_c[:, 1], Y_c[:, 1])[0, 1])


Text(0.5, 1.0, 'Comp. 2, corr = 0.09')

png

ccX_df = pd.DataFrame({"CCX_1":X_c[:, 0],
                       "CCX_2":X_c[:, 1],
                       "Species":df.species.astype('category').cat.codes,
                      "Island":df.island.astype('category').cat.codes,
                      "sex":df.sex.astype('category').cat.codes,
                       "bill_length":X_mc.bill_length_mm,
                      "bill_depth":X_mc.bill_depth_mm})
corr_X_df= ccX_df.corr(method='pearson') 
print(corr_X_df.head())

plt.figure(figsize=(10,8))
X_df_lt = corr_X_df.where(np.tril(np.ones(corr_X_df.shape)).astype(np.bool))
sns.heatmap(X_df_lt,cmap="coolwarm",annot=True,fmt='.1g')
plt.tight_layout()
plt.savefig("Heatmap_Canonical_Correlates_from_X_and_data.jpg",
                    format='jpeg',
                    dpi=100)


                CCX_1         CCX_2   Species    Island       sex  \
CCX_1    1.000000e+00 -1.217716e-16  0.935057 -0.561781  0.025383   
CCX_2   -1.217716e-16  1.000000e+00 -0.078719  0.228933  0.576790   
Species  9.350575e-01 -7.871884e-02  1.000000 -0.622428  0.010964   
Island  -5.617810e-01  2.289327e-01 -0.622428  1.000000 -0.012435   
sex      2.538332e-02  5.767897e-01  0.010964 -0.012435  1.000000   

         bill_length  bill_depth  
CCX_1       0.828437   -0.734650  
CCX_2       0.560082    0.678447  
Species     0.730548   -0.740346  
Island     -0.337179    0.568031  
sex         0.344078    0.372673  


C:\Users\ADMINI~1\AppData\Local\Temp/ipykernel_24036/698194835.py:12: DeprecationWarning: `np.bool` is a deprecated alias for the builtin `bool`. To silence this warning, use `bool` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.bool_` here.
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations
  X_df_lt = corr_X_df.where(np.tril(np.ones(corr_X_df.shape)).astype(np.bool))

png



연관성 분석 = 장바구니분석

import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rules

dataset = [['Milk', 'Onion', 'Nutmeg', 'Eggs', 'Yogurt'],
           ['Onion', 'Nutmeg', 'Eggs', 'Yogurt'],
           ['Milk', 'Apple', 'Eggs'],
           ['Milk', 'Unicorn', 'Corn', 'Yogurt'],
           ['Corn', 'Onion', 'Onion', 'Ice cream', 'Eggs']]

te = TransactionEncoder()
te_ary = te.fit(dataset).transform(dataset)
df = pd.DataFrame(te_ary, columns=te.columns_)

frequent_itemsets = apriori(df, min_support=0.5, use_colnames=True)
## parameter
# max_len=3 : 아이템 조합이 3개까지 제한

frequent_itemsets # 전체 구매 데이터 중 해당 itemset이 포함된 확률
support itemsets
0 0.8 (Eggs)
1 0.6 (Milk)
2 0.6 (Onion)
3 0.6 (Yogurt)
4 0.6 (Eggs, Onion) 
association_rules(frequent_itemsets, metric="lift", min_threshold=1) # metric 기준 min_threshold 이상
antecedents consequents antecedent support consequent support support confidence lift leverage conviction
0 (Eggs) (Onion) 0.8 0.6 0.6 0.75 1.25 0.12 1.6
1 (Onion) (Eggs) 0.6 0.8 0.6 1.00 1.25 0.12 inf

첫 줄 해석

요인분석

from sklearn.datasets import load_digits
X, _ = load_digits(return_X_y=True)

X.shape

(1797, 64)

X

array([[ 0.,  0.,  5., ...,  0.,  0.,  0.],
       [ 0.,  0.,  0., ..., 10.,  0.,  0.],
       [ 0.,  0.,  0., ..., 16.,  9.,  0.],
       ...,
       [ 0.,  0.,  1., ...,  6.,  0.,  0.],
       [ 0.,  0.,  2., ..., 12.,  0.,  0.],
       [ 0.,  0., 10., ..., 12.,  1.,  0.]])

from sklearn.decomposition import FactorAnalysis
transformer = FactorAnalysis(n_components=5, random_state=0)
X_transformed = transformer.fit_transform(X)
X_transformed.shape

(1797, 5)

X_transformed

array([[-0.15740939,  0.30545241,  1.88630105,  0.89678859, -0.17029374],
       [-0.87586253,  0.13827044, -1.75345561, -0.83281075, -0.74288303],
       [-0.99892214, -0.43236642, -1.22222905, -0.82192628, -0.77094974],
       ...,
       [-0.70066938,  0.09868465, -0.99651414, -0.14234655, -0.61502155],
       [-0.37322424, -0.18103725,  1.07294051, -0.6538424 , -0.28351881],
       [ 0.64021206, -0.87404644, -0.04237855,  0.32160612, -0.47697811]])

# ...