bskyvision blog datascienceschool
통계분석_7 - SVM (Support Vector Machine)
- 분류(SVC 사용), 회귀(SVR 사용)
※ 아래 내용 정리는 SVC 기준
- 하이퍼파라미터 : 매개변수 C와 gamma. grid search
- 매개변수들이 SVM 내에서 어떤 역할을 하는지 의미를 알고 grid search를 진행한다면 좀 더 빠르게 적합한 매개변수값들을 찾아낼 수 있음
- grid search : 매개변수들의 여러 조합들을 테스트해서 가장 좋은 성능을 내는 매개변수를 찾아내는 것
SVM 특징
커널 서포트 벡터 머신은 강력한 모델이며 다양한 데이터셋에서 잘 작동합니다.
SVM은 데이터의 특성이 몇 개 안 되더라도 복잡한 결정 경계를 만들 수 있습니다.
저차원과 고차원의 데이터(즉 특성이 적을 때와 많을 때)에 모두 잘 작동하지만 샘플이 많을 때는 잘 맞지 않습니다.
10,000개의 샘플 정도면 SVM 모델이 잘 작동하겠지만 100,000개 이상의 데이터셋에서는 속도와 메모리 관점에서 도전적인 과제입니다.
SVM의 또 하나의 단점은 데이터 전처리와 매개변수 설정에 신경을 많이 써야 한다는 점입니다.
그래서 요즘엔 사람들 대부분이 랜덤 포레스트나 그래디언트 부스팅 같은
(전처리가 거의 또는 전혀 필요 없는) 트리 기반 모델을 애플리케이션에 많이 사용합니다.
더군다나 SVM 모델은 분석하기도 어렵습니다.
예측이 어떻게 결정되었는지 이해하기 어렵고 비전문가에게 모델을 설명하기가 난해합니다.
하지만 모든 특성이 비슷한 단위이고(예를 들면 모든 값이 픽셀의 컬러 강도) 스케일이 비슷하면 SVM을 시도해볼 만합니다.
SVC vs LinearSVC
LinearSVC는 SVC보다 많은 샘플 데이터에서 선호된다고 언급되어 있고,<br>
실제로 샘플의 수가 충분히 크지 않으면, 특징이 아무리 많더라도 SVC를 사용하는 것이 좋은 것으로 확인됨<br>
그런데 충분히 크다의 의미가...... 샘플 569개, 특징 30개에서 LinearSVC가 빠르고, 샘플165개, 특징16603개에서 SVC가 빠른건......<br><br>
- SVC(support vector classifier) class의 파라미터 : kernel(kernel 지정), C(슬랙변수 가중치(slack variable weight)를 선택)
서포트 벡터 머신(SVM)
SVC in sklearn
gamma 매개변수의 기본값은 'auto'이며 이 값의 의미는 특성 개수의 역수. 즉 1/X_train.shape[1]<br>
predict_proba 함수를 가지고 있지만, 모델 생성시 probalility=True를 설정하지 않으면 사용할 수 없음<br>
import numpy as np
X = np.array([[-1, -1],
[-2, -1],
[ 1, 1],
[ 2, 1]])
y = np.array([0, 0, 1, 1])
from sklearn.svm import SVC
model = SVC(kernel='rbf', probability=True)
model.fit(X,y)
prob = model.predict_proba([[-0.8, -1]])
print('Prob[0]: %.3f' % prob[0][0])
print('Prob[1]: %.3f' % prob[0][1])
Kernel 파라미터
kernel = "linear" : 선형 SVM. k(x1,x2)=xT1x2<br>
kernel = "poly" : 다항 커널(Polynomial Kernel). k(x1,x2)=(γ(xT1x2)+θ)d<br>
kernel = "rbf" 또는 kernel = None : RBF(Radial Basis Function) 또는 가우시안 커널(Gaussian Kernel). k(x1,x2)=exp(−γ||x1−x2||2)<br>
kernel = "sigmoid" : 시그모이드 커널(Sigmoid Kernel). k(x1,x2)=tanh(γ(xT1x2)+θ)<br>
※ γ(gamma), θ(coef0), d(degree)<br>
※ RBF커널이 가장 많이 사용됨<br><br>
모델 속성
n_support_: 각 클래스의 서포트의 개수<br>
support_: 각 클래스의 서포트의 인덱스<br>
support_vectors_: 각 클래스의 서포트의 x 값. x+와 x−<br>
coef_: w 벡터<br>
intercept_: −w0<br>
dual_coef_: 각 원소가 ai⋅yi로 이루어진 벡터, 서포트 벡터<br><br>
예시
from sklearn.svm import SVC<br>
model = SVC(kernel='linear', C=1e10).fit(X, y)<br>
model.n_support_<br>
선형 서포트 벡터 머신(LinearSVM)

- 데이터를 선형으로 분리하는 최적의 선형 결정 경계를 찾는 알고리즘
- 클래스가 다른 데이터들을 가장 큰 마진(margin)으로 분리해내는 선 또는 면(결정 경계)을 찾아내는 것
LinearSVC in sklearn
SVC에서 kernel='linear'인 분류 모델<br>
손실함수 default는 제곱 힌지(squared hinge), C의 default는 1.0<br>
선형 계산에 특화되어 있어 SVC를 이용하는 것보다 더 효율적인 성능을 보여줌<br>
predict_proba를 전혀 제공하지 않음<br>
SVC 또는 다른 분류 모델처럼 각 클래스에 대한 확률값(prob)을 얻으려면 사용자가 소스코드를 구현해야함<br>
그마저도 이진분류에서만 가능하므로 레이블이 3개 이상인 경우, LinearSVC보단 SVC를 사용하고 probability=True 옵션 주는 것을 추천<br>
매개변수 : C(Cost)
**이상치(outlier)**들이 있을 경우 데이터들을 선형적으로 완벽하게 분리하는 것은 불가능함<br>
이를 해결하기 위해 약간의 오류를 허용하는 전략이 만들어졌고, 이와 관련된 파라미터가 C임<br>
C는 **얼마나 많은 데이터 샘플이 다른 클래스에 놓이는 것을 허용하는지**를 결정함(L2 규제의 강도를 결정)<br>
C가 **작을수록 많이 허용**하고, 클수록 규제가 감소하여 적게 허용함<br>
C가 **너무 낮으면 과소적합**될 가능성이 커지고, C가 너무 높으면 과대적합될 가능성이 커짐<br>
C의 유무에 따라 **없으면 hard-margin SVM**, 있으면 soft-margin SVM으로 나뉨<br>
import pandas as pd
import numpy as np
# 시각화
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style("whitegrid")
# 그래프 한글폰트 깨짐 방지
#path="c:/Windows/Fonts/malgun.ttf"
path="C:/Users/BOBO/Documents/Python/malgun.ttf"
from matplotlib import font_manager, rc
#help(matplotlib.font_manager)
font_name = font_manager.FontProperties(fname=path).get_name()
plt.rc('font', family=font_name)
#plt.rc('font', family='Malgun Gothic')
import mglearn ## pip install mglearn
# 데이터셋 만들기
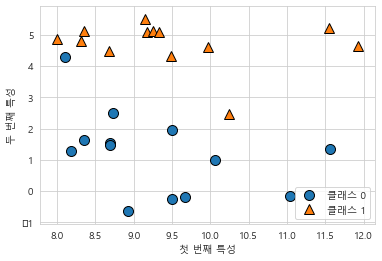
# forge 데이터셋 : 두개의 특성을 가진 데이터셋으로 인위적으로 만든 이진 분류 데이터셋
X, y = mglearn.datasets.make_forge()
# 산점도 그리기
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.legend(["클래스 0", "클래스 1"], loc=4)
plt.xlabel("첫 번째 특성")
plt.ylabel("두 번째 특성")
print("X.shape: {}".format(X.shape))
> X.shape: (26, 2)
# from sklearn.datasets import make_blobs
# X, y = make_blobs(n_samples=50, centers=2, cluster_std=0.5, random_state=4)
# y = 2 * y - 1
# plt.scatter(X[y == -1, 0], X[y == -1, 1], marker='o', label="-1 클래스")
# plt.scatter(X[y == +1, 0], X[y == +1, 1], marker='x', label="+1 클래스")
# plt.xlabel("x1")
# plt.ylabel("x2")
# plt.legend()
# plt.title("학습용 데이터")
# plt.show()
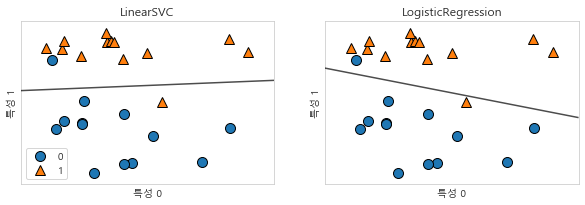
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
clf = model.fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5, ax=ax, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{}".format(clf.__class__.__name__))
ax.set_xlabel("특성 0")
ax.set_ylabel("특성 1")
axes[0].legend()
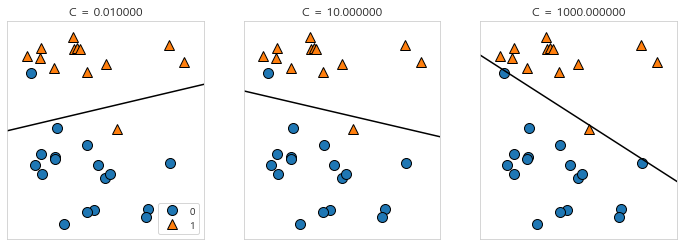
# 매개변수 C에 따른 결정 경계
mglearn.plots.plot_linear_svc_regularization()
# C가 커질수록 현재 데이터는 더 잘 분류하였으나 과대 적합 가능성
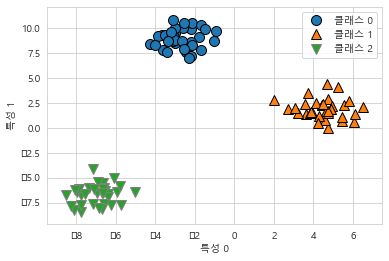
다중 클래스 분류
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(["클래스 0", "클래스 1", "클래스 2"])
# LinearSVC fit
linear_svm = LinearSVC().fit(X, y)
print("계수 배열의 크기: ", linear_svm.coef_.shape)
print("절편 배열의 크기: ", linear_svm.intercept_.shape)
> 계수 배열의 크기: (3, 2)
절편 배열의 크기: (3,)
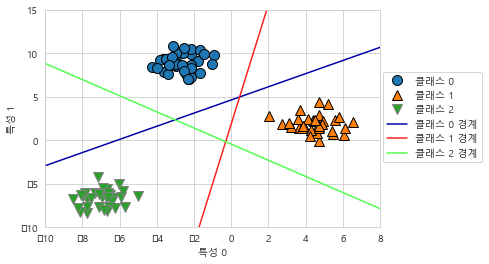
# 세 개의 이진 분류기가 만드는 경계를 시각화
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계',
'클래스 2 경계'], loc=(1.01, 0.3))
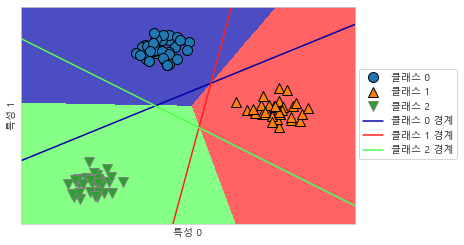
# 2차원 평면의 모든 포인트에 대한 예측 결과
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계',
'클래스 2 경계'], loc=(1.01, 0.3))
plt.xlabel("특성 0")
plt.ylabel("특성 1")
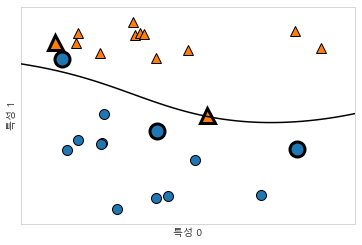
커널 서포트 벡터 머신(SVM)
- SVM은 선형 SVM이든 RBF 커널 SVM이든 항상 선형으로 데이터를 분류하는 것이 기본적인 전략
- 입력 데이터에서 단순한 초평면(hyperplane)으로 정의되지 않는 더 복잡한 모델을 만들 수 있도록 확장한 것
- 커널 기법은 주어진 데이터를 고차원 특징 공간으로 사상해주는 것으로, 고차원 공간에 사상되고 나면 원래의 차원에서는 보이지 않던 선형으로 분류 가능
- 비선형 결정 경계
매개변수 : C와 gamma
- C
선형 모델에서 사용한 것과 비슷한 규제 매개변수
각 포인트의 중요도(dual_coef_ 값)을 제한함
- gamma
하나의 훈련 샘플이 미치는 영향의 범위를 결정
작은 값은 넓은 영역을 의미하며 큰 값일 경우 영향이 미치는 범위가 제한적
가우시안 커널의 반경이 클수록 훈련 샘플의 영향 범위도 커짐
from sklearn.svm import SVC
import mglearn ## pip install mglearn
# 데이터셋 만들기
# forge 데이터셋 : 두개의 특성을 가진 데이터셋으로 인위적으로 만든 이진 분류 데이터셋
X, y = mglearn.datasets.make_forge()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
# 서포트 벡터
sv = svm.support_vectors_
# dual_coef_의 부호에 의해 서포트 벡터의 클래스 레이블이 결정됩니다.
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15, markeredgewidth=3)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
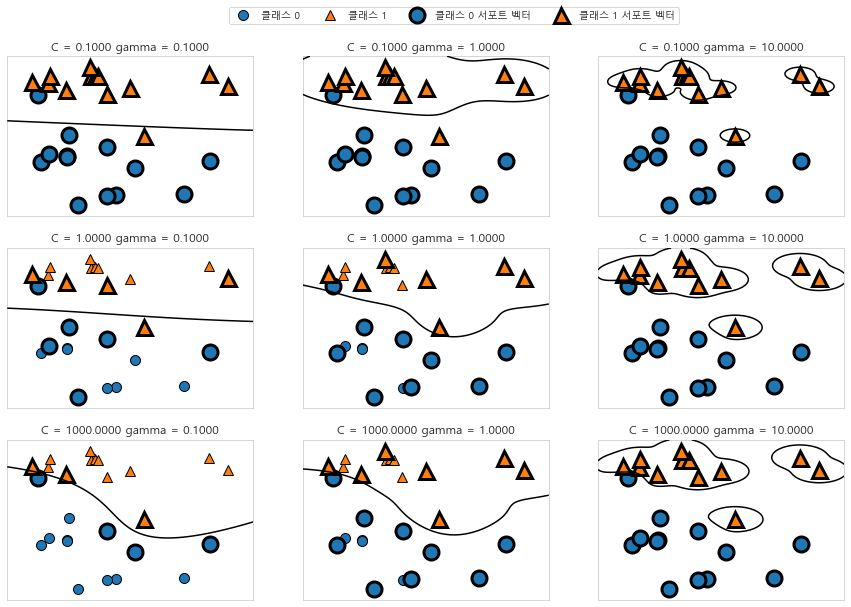
# 매개변수 gamma 튜닝
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]):
for a, gamma in zip(ax, range(-1, 2)):
mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["클래스 0", "클래스 1", "클래스 0 서포트 벡터", "클래스 1 서포트 벡터"],
ncol=4, loc=(.9, 1.2))
# 오른쪽으로 갈수록 gamma 증가시키고 아래로 갈수록 C 증가시킴
# gamma가 클수록 복잡한 모델을 만듦
# C가 클수록 현재 데이터를 정확하게 분류
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
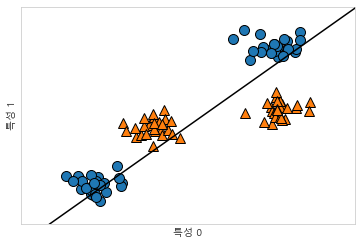
# 선형SVM으로 만든 결정 경계(맞지않음)
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
유방암 데이터셋 분류하기(RBF커널 SVM)
- 유방암 종양의 임상 데이터를 기록해놓은 위스콘신 유방암Wisconsin Breast Cancer 데이터셋
- 각 종양은 양성benign(해롭지 않은 종양)과 악성malignant(암 종양)으로 레이블되어 있고, 조직 데이터를 기반으로 종양이 악성인지를 예측할 수 있도록 학습하는 것이 과제
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
print("cancer.keys(): \n{}".format(cancer.keys()))
print("유방암 데이터의 형태: {}".format(cancer.data.shape))
print("클래스별 샘플 개수:\n{}".format(
{n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))
print("특성 이름:\n{}".format(cancer.feature_names))
> cancer.keys():
dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
> 유방암 데이터의 형태: (569, 30)
> 클래스별 샘플 개수:
{'malignant': 212, 'benign': 357}
> 특성 이름:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=0, test_size=0.25)
#default : C=1, kernel='rbf', gamme='auto'(1/n_features)
svc = SVC(random_state=0)
svc.fit(X_train, y_train)
print("훈련 세트 정확도: {:.2f}".format(svc.score(X_train, y_train)))
print("테스트 세트 정확도: {:.2f}".format(svc.score(X_test, y_test)))
> 훈련 세트 정확도: 0.90
> 테스트 세트 정확도: 0.94
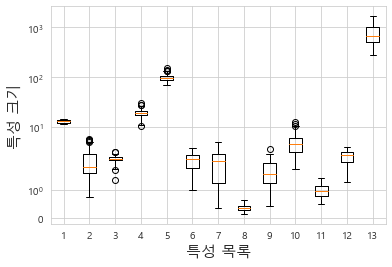
# SVM은 잘 작동하는 편이지만 매개변수 설정과 데이터 스케일에 매우 민감
# 특히 입력 특성의 범위가 비슷해야 합니다. 각 특성의 최솟값과 최댓값을 로그 스케일로 나타내보겠습니다
plt.boxplot(x_train)
plt.yscale('symlog') # y축 로그 스케일
plt.xlabel('특성 목록', size =15)
plt.ylabel('특성 크기', size =15)
plt.show()
# 특성의 크기가 매우 다름 -> SVM은 영향을 크게 받음 -> 전처리(MinMaxScaler) 필요
# 전처리(MinMaxScaler)
# X_train에서 특성별 최솟값 계산
min_on_training = X_train.min(axis=0)
# X_train에서 특성별 (최댓값 - 최솟값) 범위 계산
range_on_training = (X_train - min_on_training).max(axis=0)
# X_train에 최솟값을 빼고 범위로 나누면 각 특성에 대해 최솟값은 0, 최대값은 1
X_train_scaled = (X_train - min_on_training) / range_on_training
print("특성별 최소 값\n{}".format(X_train_scaled.min(axis=0)))
print("특성별 최대 값\n {}".format(X_train_scaled.max(axis=0)))
> 특성별 최소 값
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0.]
> 특성별 최대 값
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1.]
# X_test에도 같은 작업을 적용(X_train에서 계산한 최솟값과 범위를 사용)
X_test_scaled = (X_test - min_on_training) / range_on_training
svc = SVC()
svc.fit(X_train_scaled, y_train)
print("훈련 세트 정확도: {:.3f}".format(
svc.score(X_train_scaled, y_train)))
print("테스트 세트 정확도: {:.3f}".format(svc.score(X_test_scaled, y_test)))
> 훈련 세트 정확도: 0.984
> 테스트 세트 정확도: 0.972
# 매개변수 튜닝(C값 증가)
svc = SVC(C=1000)
svc.fit(X_train_scaled, y_train)
print("훈련 세트 정확도: {:.3f}".format(svc.score(X_train_scaled, y_train)))
print("테스트 세트 정확도: {:.3f}".format(svc.score(X_test_scaled, y_test)))
> 훈련 세트 정확도: 1.000
> 테스트 세트 정확도: 0.958